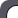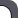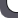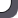;;;…;;… - члены ряда;      - n-ый или общий член ряда

Если члены ряда - числа, то ряд называется числовым;

Если члены ряда - числа одного знака, то ряд называется знакопостоянным;

Если члены ряда - числа разных знаков, то ряд называется знакопеременным;

Если члены ряда - положительные числа, то ряд называется знакоположительным;

Если члены ряда - числа, знаки которых строго чередуются, то ряд называется знакочередующимся

Если члены ряда - функции, то ряд называется функциональным;

Если члены ряда - степени х - то ряд называется степенным

Если члены ряд - тригонометрические функции, то ряд называется тригонометрическим.

Ряд может быть сходящимся и расходящимся.
Если бесконечная сумма является конечным числом, то ряд называют сходящимся
Если бесконечная сумма равна бесконечности, то ряд назыывают расходящимся

Вообще говоря, для определения сходимости вовсе не нужно находить сумму ряда, чаще пользуются специальными признаками сходимости. Именно благодаря им можно выяснить, сходится ряд или нет

ОСНОВНЫЕ ПРИЗНАКИ СХОДИМОСТИ:

1) необходимый признак сходимости
2) признаки сравнения
3) признак Даламбера
4) признак Коши
5) нтегральный признак

 

 

 

Числовые ряды
№1


Степенные ряды
№1     №2